Arcane Connections

The impact of truly fundamental results in a given subfield of science always extends well beyond that subfield.  Suddenly a new, unfathomed connection may pop up between areas previously believed to be totally disjointed, an occurrence that never fails to make one gasp in amazement.  Long appreciated by mathematicians, discoveries of this type occur in theoretical physics and statistical mechanics as well.  The work recently co-authored by ICTP Emeritus Scientist Vladimir Kravtsov (former head of the Condensed Matter and Statistical Physics section), is in this very exclusive class.

The two fields in this case could hardly be further apart.

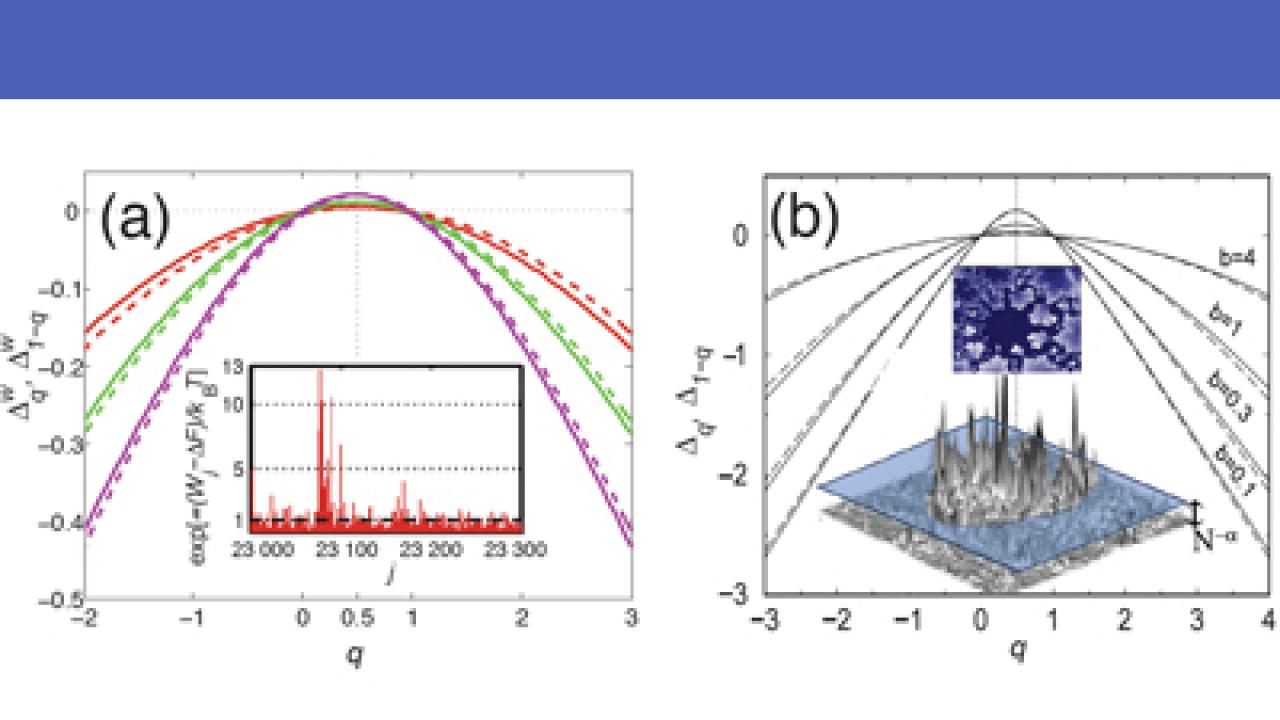
The first field is exquisitely quantum-mechanical and time-independent, concerning the statistical properties of wave functions for electrons moving in a random potential, when tuned in such a way to critically approach the celebrated metal-insulator transition invented by P.W. Anderson in 1958. Poised on the brink between exponentially localized states of the insulator and the extended states of the metal, the critical wave functions are "multifractal",  sharing properties of both sides in a weird, fascinating, and only partly understood fashion that has only gradually been unveiled in the last two decades.

The second field has nothing to do with quantum mechanics or time independence. It concerns the random distribution of work done when pushing many different times, e.g. mechanically or electrically, a small system from a state A to a state B. Classical non-equilibrium statistical mechanics being the well established field it has become in the last century, the discovery of the new Jarzynski-Crooks theorems during the last two decades came as a surprise to many. They stated that the probability distribution of frictional work must satisfy some exact exponential identities, which implied, amazingly, that at least sometimes the frictional part of the work spent must be negative, although of course always positive on average, lest the second principle of thermodynamics be violated.

Within simple assumptions, the new work strikingly maps one problem smack onto the other, down to the finest mathematical detail, and including an experimental verification. Because the level of development of the two fields is not the same, suddenly the mathematics and the understanding that was developed for one immediately applies to the other. Both fields will move forward as a result. Arcane as this connection may seem at first, it does represent a far reaching, milestone contribution.

The work, titled "Multifractality of random eigenfunctions and generalization of Jarzynski equality", (DOI 10.1038/ncomms8010), was published by Nature Communications on 27 April.

--Erio Tosatti